연결 그래프

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 꼭짓점 연결성 (점 연결도)
- 2.2. 변 연결성
3. 유향 그래프와 연결도
4. 성질
5. 관련 알고리즘
6. 일반화
7. 예
참조

1. 개요

연결 그래프는 그래프의 임의의 두 꼭짓점 사이에 경로가 존재하는 그래프를 의미한다. 그래프가 얼마나 튼튼하게 연결되어 있는지를 나타내는 척도로 점 연결도와 변 연결도가 있으며, 유향 그래프에서는 강연결, 점 강연결도, 유향 변 강결합도 등의 개념이 사용된다. 연결 그래프의 성질과 관련된 다양한 정리와 알고리즘이 존재하며, 단절도, 정점 영역 연결도, 집합 간 연결도 등으로 일반화될 수 있다.

2. 정의

그래프의 서로 다른 두 꼭짓점 $u,v$ 에 대하여, $u$ 와 $v$ 사이의 경로가 존재하면 두 꼭짓점은 '''연결되었다'''(connected^영어)고 한다.

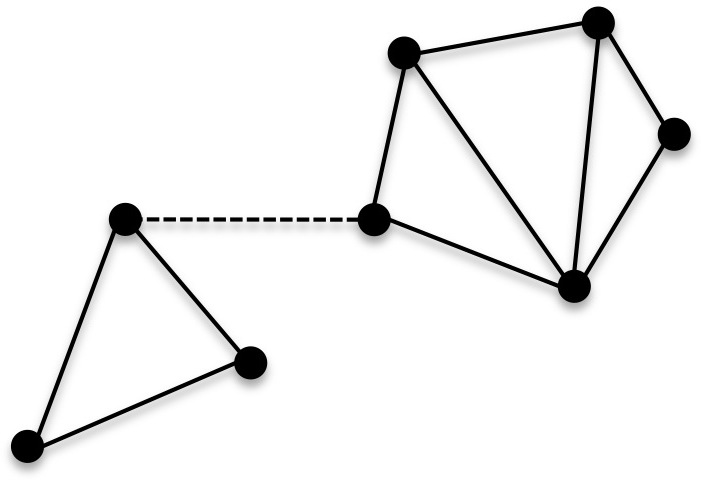
'''연결 그래프'''(connected graph^영어)는 임의의 서로 다른 두 꼭짓점이 연결된 그래프이다. 그래프의 '''연결 성분'''(connected component^영어)은 (포함 관계에 대한) 극대 연결 부분 그래프이다.

그래프가 얼마나 튼튼하게 연결되어 있는지를 나타내는 불변량으로 연결도가 있으며, 주로 점 연결도와 변 연결도로 분류된다.

2. 1. 꼭짓점 연결성 (점 연결도)

그래프

G

에서 제거하면 비연결 그래프가 되는

k

개의 정점 집합을 '''

k

-점 절단'''이라고 한다.

G

에서

k

-점 절단이 존재하는 최소의

k

를 '''점 연결도''' 또는 연결도라고 하며,

\kappa(G)

또는

\chi(G)

로 나타낸다. 특히, 1-점 절단을 '''절단점''' 또는 '''관절점'''이라고 부른다.

k

-연결 그래프는 점 연결도가

k

이상인 그래프이다.

그래프

G

에서

S

를 제거한 그래프에서

x

와

y

사이에 경로가 존재하지 않는 것을 정점 집합

S

가

x, y

를 '''분리'''한다고 한다. 그래프

G

에서 (만약 존재한다면) 변

xy

를 제거한 그래프에서 두 정점

x, y

를 분리하는 데 필요한 정점의 개수를

s

라고 할 때,

x, y

가 인접하지 않으면

s

를,

x, y

가 인접해 있으면

s + 1

을

x, y

의 '''국소 연결도'''라고 하며, 보통

\kappa(x, y)

로 나타낸다. 점 연결도는 국소 연결도의 최솟값과 일치한다.

그래프

G

의 어떤 인자가

k

연결이면,

G

자신도

k

연결이 된다.

G

가

k

연결이고,

G

자신을 제외한 인자가

k

연결이 아닐 때 (즉,

G

에서 변을 하나라도 제거하면

k

연결이 아닐 때),

G

를 '''극소

k

연결'''이라고 한다.

2. 2. 변 연결성

그래프에서 제거하면 비연결 그래프가 되는 k개의 변 집합을 '''k-변 절단''' (또는 k-컷)이라고 한다. k-변 절단이 존재하는 최소의 k를 '''변 연결도'''라고 하며,

\lambda(G), \chi'(G)

로 표기한다.^[1] 특히, 1-변 절단을 '''절단 변''' 또는 '''다리'''(bridge^영어)라고 한다.^[1] k-변 연결 그래프는 변 연결도가 k 이상인 그래프를 가리킨다.^[1]

두 점을 분리하는 변 집합 크기의 최솟값으로 '''국소 변 연결도'''가 정의되며

\lambda(x, y)

로 표기된다.^[1]

또한,

\lambda(G) = \min_{x, y \in V(G)} \lambda(x, y)

가 됨을 덧붙여 둔다.^[1]

3. 유향 그래프와 연결도

유향 그래프에서도 무향 그래프에서처럼 연결도에 해당하는 개념을 정의할 수 있다.^[1]

3. 1. 강연결

유향 그래프가 '''강결합'''이라는 것은, 그래프 상의 임의의 두 점 사이에 유향 경로가 존재하는 것이다. 극대 강결합 부분 그래프는 '''강결합 성분'''이라고 한다.

3. 2. 점 강연결도

어떤 두 점 를 지정했을 때, 제거함으로써 중 어느 쪽을 시작점으로 하더라도 유향 경로가 존재하지 않게 되는 점 집합의 크기의 최솟값으로, 의 국소 점 강연결도 (''local vertex-strong connectivity'')가 정의된다. 또한, 국소 점 강연결도의 최솟값을 점 강결합도 (''vertex-strong connectivity'')라고 부른다. 점 강결합도가 이상인 그래프를 점 강결합 그래프 (-''strongly connected graph'') 또는 강 그래프 (-''strong graph'')라고 부른다.

3. 3. 유향 변 강연결도

어떤 두 점 를 지정했을 때, 제거함으로써 의 어느 쪽을 시작점으로 해도 유향 경로가 존재하지 않게 되는 변 집합의 크기 최소값을 의 국소 유향 변 강결합도라고 정의한다. 또한, 국소 유향 변 강결합도의 최소값을 유향 변 강결합도라고 부른다. 유향 변 강결합도가 이상인 그래프를 유향 변 강결합 그래프 또는 유향 변 강 그래프라고 부른다.

4. 성질

그래프 $G$ 에 대하여 다음이 성립한다.^[2]

: $\kappa(G)\le\lambda(G)\le\min_{v\in V(G)}\deg v$

그래프 $G$ 의 최소 차수를 $\delta(G)$ 로 나타내면, $\kappa(G) \leqq \lambda(G) \leqq \delta(G)$ 이다.
임의의 $l 에 대해, \kappa(G)=l, \lambda(G)=m, \delta(G)=n 을 만족하는 그래프 G 가 존재한다.$
2-연결 그래프의 임의의 정점은 사이클 위에 있다.
두 점 $x, y$ 사이의 서로 독립적인 경로 (점소 패스)의 최대 개수는 국소 연결도 $\kappa(x, y)$ 와 일치한다 (멩거 정리).
두 점 $x, y$ 사이의 변소 패스의 최대 개수는 국소 변 연결도 $\lambda(x, y)$ 와 일치한다 (멩거 정리).
임의의 $k$ 차원 다면체의 그래프의 정점 연결도는 $k$ 이다 (발린스키의 정리).

5. 관련 알고리즘

k-정점 연결 요소 분해
k-간선 연결 요소 분해
강결합 요소 분해

6. 일반화

단절점
정점 영역 연결도
집합 간 연결도

7. 예

wikitext

간단한 그래프의 꼭짓점·변 연결성은 다음과 같다.

그래프	꼭짓점 연결성	변 연결성
비연결 그래프	0	0
완전 그래프 $K_n$ ( $n\ge1$ )	$n-1$	$n-1$
나무 (꼭짓점 2개 이상)	1	1
순환 그래프 $C_n$ ( $n\ge3$ )	2	2
라도 그래프	$\aleph_0$	$\aleph_0$

참조

_[1] 문서 점連結度の対応物と辺連結度の対応物についての用語の和訳は定訳が不明であるため直訳した。
_[2] 서적 Algebraic graph theory Springer 2001

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com